4 Divide-and-Conquer
“To iterate is human, to recurse divine.”
– L Peter Deutsch
Exercise 4.1 Try the keyword recursion in Google search.
Google recursively asks: “Did you mean recursion”!!
So far in this course, we discussed three sorting techniques: selection, insertion, and bubble sort. For all of them, the running time in the worst-case is O(n^2), where n is the size of the input array. You may be wondering if we can design an algorithm that can outperform these sorting techniques.
Well, the answer is yes. Until now, we have only seen incremental algorithms. In this chapter, we will see a different paradigm, known as recursive algorithms, and they typically follow the divide-and-conquer method. Employing divide-and-conquer, we will develop merge sort—a sorting algorithm that runs in O(n\lg{n})-time.
Exercise 4.2 Why O(n\lg{n}) is better than O(n^2)?
In terms of upper bounds, the function n\lg{n} is also O(n^2). If T(n) denotes the running time of MERGE-SORT, then T(n) is both O(n\lg{n}) and O(n^2). However, the former is a much stronger upper bound. It guarantees less computational steps than O(n^2); see Figure 3.1 for reference.
4.1 Recursive Algorithms
In divide-and-conquer, we typically break a computational problem into several subproblems that are similar in structure to the original problem but smaller in size. We then solve these subproblems recursively, to finally combine the these solutions to create a solution to the original problem.
When a subproblem gets small enough—the base case—you just solve it directly without recursing. Otherwise—the recursive case—you perform three characteristic steps:
Divide the (sub)problem into one or more subproblems that are smaller instances of the same problem.
Conquer the subproblems by solving them recursively.
Combine the subproblem solutions to form a solution to the original problem.
Solutions that use divide-and-conquer are implemented using recursive algorithms. While incremental algorithms are easy to design, understand, and analyze, recursive algorithms may not always seem to be intuitive at first glance. The reason is human beings do not think recursively! Moreover, the design and analysis of running times of recursive algorithms can be a bit challenging. We discuss two techniques in this chapter to facilitate easy computation of their running times.
4.2 Some Basic Examples
Let us rethink some of the basic computational problems, some of which we may have previously solved using incremental algorithms.
Factorial
The most straight-forward algorithm for computing the factorial of a positive integer n\geq1 is incremental.
In order to design a recursive algorithm, we need to find a way to divide the factorial problem into similar instances but smaller in size. What can help is the following mathematical fact: n! = n\times (n-1)!\text{ for any }n\geq1.
The equation is, in fact, recursive. In light of the equation, we now devise our divide-and-conquer strategy:
Divide: Find the factorial of (n-1).
Conquer: Compute (n-1)! recursively. The recursion reaches the base case, when n=1, to return 1.
Combine: We use the recursive formula: n! = n\times (n-1)! to compute the factorial of n from the factorial of (n-1).
Here is the pseudocode of REC-FACTORIAL:
Exercise 4.3 Implement REC-FACTORIAL in Python. Run it for n=10.
Fibonacci Numbers
The Fibonacci sequence is a sequence of numbers is which each number (except for the first two) is the sum of the previous two numbers. Conventionally, the first two numbers are assumed to be 0 and 1.
Exercise 4.4 Design a recursive algorithm to find the n-th Fibonacci number for any n\geq0. For example, when n=4, the output is 3. Clearly state how you would divide, conquer, and combine.
In order to design a recursive algorithm, we note from the definition: \text{fib}(n) = \text{fib}(n-1)+\text{fib}(n-2)\text{ for any }n\geq2, and \text{fib}(0)=0 and \text{fib}(1)=1.
The equation is, in fact, recursive. In light of the equation, we now devise our divide-and-conquer strategy:
Divide: Find the numbers \text{fib}(n-1) and \text{fib}(n-2).
Conquer: Compute \text{fib}(n-1) and \text{fib}(n-2) recursively. The recursion reaches the base case—when n=0 or n=1—to return 0 or 1, respectively.
Combine: We use the recursive formula: \text{fib}(n) = \text{fib}(n-1)+\text{fib}(n-2) to compute the n-th Fibonacci number \text{fib}(n) adding \text{fib}(n-1) and \text{fib}(n-2).
Exercise 4.5 Write a pseudocode for REC-FIB.
Exercise 4.6 Implement REC-FIB in Python. Run your code for n=4, n=10, and n=50.
Exercise 4.7 For n=50, why does it take forever to run REC-FIB?
Essentially, REC-FIB is an exponential algorithm, i.e., in the order of 2^n. This is due to a significant amount of over-computation. For example, \text{Fib}(10) (recursively) computes \text{Fib}(9) and \text{Fib}(8). In order to compute \text{Fib}(9), it again computes \text{Fib}(8)! This way most of the branches of the recursion tree are unnecessarily repeated, giving rise to an exponentially growing algorithm.
The incremental algorithm for Fibonacci numbers is way more efficient. In fact, it is still O(n).
4.3 Merge Sort
In order to design a recursive algorithm for sorting, we use the following divide-and-conquer strategy:
Divide: the subarray A[p:r] to be sorted into two adjacent subarrays, each of (almost) half the size. To do so, compute the midpoint q of A[p:r] (taking the average of p and r), and divide A[p:r] into subarrays A[p:q] and A[q+1:r].
Conquer: by sorting each of the two subarrays A[p:q] and A[q+1:r] recursively using MERGE-SORT. The recursion—bottoms out—it reaches the base case—when the subarray to be sorted has just 1 element, that is, when p equals r.
Combine: by merging (MERGE) the two sorted subarrays A[p:q] and A[q+1:r] back into A[p:r], producing the sorted answer.
We present a pseudocode of MERGE-SORT:
Note that the code calls the MERGE algorithm as described here.
Exercise 4.8 Dry-run MERGE-SORT on the input <3, 2, 5, -1, 0, 1, -2, 4>.
Exercise 4.9 Implement MERGE-SORT in Python.
Exercise 4.10 Is there any best (or worst) case input for MERGE-SORT.
No.
Exercise 4.11 Run MERGE-SORT for the worst-case input of INSERTION-SORT and n=1,000,000. See for yourself which algorithm performs better.
4.4 Binary Search
We have already observed in SEARCH-ARRAY that searching takes O(n). However, if the array is already sorted, we can improve the algorithm for a better worst-case running time.
Exercise 4.12 Assuming that the input array A[0:n-1] is already sorted, what would you infer about the location of the query value x if the midpoint element of A is smaller than x?
We can disregard the first half of the array for further consideration, and search only the second half of the array.
Exercise 4.13 Using the insights from the previous exercise, design a recursive algorithm to solve the searching problem. I am sure what you would come up with is already known as the binary search algorithm. Write a pseudocode for BIN-SEARCH.
Exercise 4.14 Implement BIN-SEARCH in Python.
Exercise 4.15 Modify the binary search algorithm to divide the array into three (almost equal) pieces instead of two; call it TERNARY-SEARCH. Write down a Python implementation of TERNARY-SEARCH.
4.5 Analyzing Recursive Algorithms
One of the disadvantages of recursive algorithms is their running times can often be difficult to compute. Sometimes, their running time T(n) can be described by a recursive equation or recurrence. A recurrence is a special equation that contains the definition of one the variables in terms of itself. In fact, this is the expected pattern when we see keywords like recursion, recursive, or divide-and-conquer!
Recurrence Equation
The three steps of the underlying divide-and-conquer method can help establish such an equation for a recursive algorithm. In the base case, the problem size is small enough, say n<n_0 for some constant n_0, then it should take constant time c_0. So, T(n) = c_1\text{ for }n<n_0.
In the recursive case, n>n_0 and we divide the problem into, say a subproblems, each with size n/b. So, T(n) must be the sum of the running times of these subproblems, plus the cost of dividing and combining them. Due to the reduced size, note that the running time of each subproblem is T(n/b). Since the original problem is divided into a many subproblems, we can write T(n) = D(n) + aT(n/b) + C(n)\text{ for }n\geq n_0, where D(n) and C(n) denote the costs of dividing the original problem and combining the solved subproblems, respectively.
Therefore, the recurrence can be written as T(n)=\begin{cases} c_0&\text{ if }n<n_0 \\ D(n) + aT(n/b)+C(n)&\text{ if }n\geq n_0 \end{cases}
In order to solve such a recursion, there are two commonly used approaches: recursion tree and Master Theorem. Before we present these methods in the next subsection, we first try to set up the recurrences for the problems we already solved.
BIN-SEARCH
We take, for example, the BIN-SEARCH algorithm. Here is how to set up the recurrence for the running time T(n) of BIN-SEARCH on n numbers.
Divide: This step just computes the middle of the subarray, which is assumed to take constant time c_1. So, D(n)=c_1.
Conquer: Recursively solving one subproblem with size n/2, contributes T(n/2) to the running time. So, a=1 and b=2.
Combine: In BIN-SEARCH, we are not really combining anything—just returning the value. So, this step takes constant time c_2. So, C(n)=c_2.
Adding these contributes together, we get the recurrence: T(n)=\begin{cases} c_0&\text{ if }n=1 \\ c_1 + T(n/2) + c_2&\text{ if }n>1 \end{cases} Combining the constant terms c_1 and c_2 into c_3, we can write: T(n)=\begin{cases} c_0&\text{ if }n=1 \\ c_3 + T(n/2)&\text{ if }n>1 \end{cases} \tag{4.1}
MERGE-SORT
Exercise 4.16 Find the recurrence for MERGE-SORT.
Here is how to set up the recurrence for the running time T(n) of MERGE-SORT on n numbers.
Divide: This step just computes the middle of the subarray, which is assumed to take constant time c_1. So, D(n)=c_1.
Conquer: Recursively solving two subproblems, each of size n/2, contributes 2T(n/2) to the running time. So, a=2 and b=2.
Combine: Since the MERGE procedure takes c_2 + c_3n, as we previously discussed. So, C(n)=c_2 + c_3n.
Adding these contributes together, we get the recurrence: T(n)=\begin{cases} c_0&\text{ if }n=1 \\ c_1 + 2T(n/2) + c_2 + c_3n&\text{ if }n>1 \end{cases} Combining the constant terms c_1 and c_2 into c_4, we can write: T(n)=\begin{cases} c_0&\text{ if }n=1 \\ c_4 + 2T(n/2) + c_3n&\text{ if }n>1 \end{cases} \tag{4.2}
Recursion Tree
This approach is more direct and visually appealing. It mimics our method of producing a cost table in case of an incremental algorithm. Instead of a table, we use a tree with costs labeled at its nodes.
In a recursion tree, each node represents the cost of a single subproblem somewhere in the set of recursive function invocations. You typically sum the costs within each level of the tree to obtain the per-level costs, and then you sum all the per-level costs to determine the total cost of all levels of the recursion.
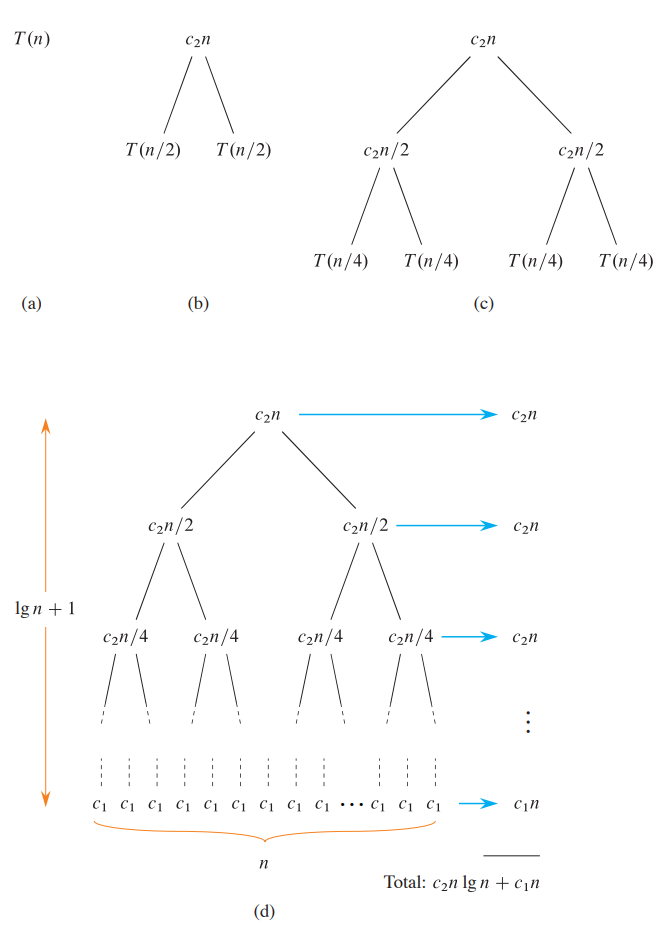
Example 4.1 (MERGE-SORT) We demonstrate the recursion tree method for MERGE-SORT.
Part (a) of the Figure shows T(n), which part (b) expands into an equivalent tree representing the recurrence. The c_2n term denotes the cost of dividing and combining at the top level of recursion, and the two subtrees of the root are the two smaller recurrences T(n/2). Part (c) shows this process carried one step further by expanding T(n/2). The cost for dividing and combining at each of the two nodes at the second level of recursion is c_2n/2. Continue to expand each node in the tree by breaking it into its constituent parts as determined by the recurrence, until the problem sizes get down to 1, each with a cost of c_1. Part (d) shows the resulting recursion tree.
Exercise 4.17 Find the running time of BIN-SEARCH by drawing a recursion tree.
Do it yourself.
Exercise 4.18 Find an upper bound solution for the recursion T(n) =\begin{cases} c_0&\text{ if }n=1\\ 3T(n/4) + c_1n^2 &\text{ if }n\geq1 \end{cases} \tag{4.3} both using a recursion tree and the direct method.
See Section 4.6.
The (Simplified) Master Theorem
We present here a simplified version of the master theorem. For the more general version, see Cormen et al. (2009).
Theorem 4.1 (The Master Theorem) Let a\geq1 and b\geq2, and let c_0, c_1,k be non-negative constants. Define the recurrence T(n) on n\in\mathbb{N} by T(n)=c_0 + aT(n/b)+c_1n^k. Then, T(n)=\begin{cases} O(n^{\log_b{a}}) &\text{ if }a>b^k \\ O(n^k\lg{n}) &\text{ if }a=b^k \\ O(n^k)&\text{ if }a<b^k \end{cases}
The master theorem is very easy to apply. We just compare a to the term b^k.
Exercise 4.19 Apply the master theorem to the recursion (Equation 4.1) for BIN-SEARCH.
In this case, we have a=1, b=1, and k=0. Therefore, T(n)=O(\lg{n}).
Exercise 4.20 Apply the master theorem to the recursion for MERGE-SORT.
In this case, we have a=2, b=2, and k=1. Therefore, T(n)=O(n\lg{n}).
Exercise 4.21 Apply the master theorem to the recursion for Equation 4.3.
In this case, we have a=3, b=4, and k=2. Therefore, T(n)=O(n^2).
Exercise 4.22 Apply the master theorem to solve T(n)=4T(n/9) + 7\sqrt{n}.
In this case, we have a=4, b=9, and k=1/2. Therefore, T(n)=O(n^{\log_9{4}}), which is roughly O(n). Think why.
Exercise 4.23 Modify the binary search algorithm to divide the array into three (almost equal) pieces instead of two; call it TERNARY-SEARCH. Write down the recurrence of TERNARY-SEARCH, and solve it using any of the above mentioned methods.
In this case, we have a=1, b=3, and k=0. Therefore, T(n)=O(\lg{n}). So, you don’t gain advantage over BIN-SEARCH.